12 July 2002
This page contains my notes from reading Stephen Wolfram's "A New Kind of Science". The notes are generally arranged in the order of the book, with the exception that common themes are brought out in a separate section, and with the proviso that the notes are read hand-in-hand with the main text.
Please note that I have put these pages together in my spare time, without access to a reference library—so my resources are limited.
This page contains material from Stephen Wolfram's "A New Kind Of Science", used without permission under fair use provisions.
Text in green has been added since the original version of this page.
[Nov 2004] The book is now generously available online, so I've tried to add the appropriate hyperlinks below.
This section contains notes on themes which occur throughout the book.
In the first half of the book, Wolfram is at great pains to point out that one "his discoveries" is the observation that simple programs can generate complex behavior. He tells us that this breaks an age-old assumption that if you observe complex behavior in a system, it must be a complex system. In fact, he continues to tell us this several times in every chapter of the book—I counted at least 35 places where he reinforces this point, usually accompanied by a declaration that this is his discovery.
However, this is not a novel observation. The most obvious area of science where an almost identical observation has been made, and loudly, for over twenty years is chaos theory. The chaos theory version of this observations is that simple (nonlinear) systems can generate complex behavior. To quote the last sentence from the important survey article by Robert May back in 1976: ". . we would all be better off if more people realised that simple nonlinear systems do not necessarily possess simple dynamical properties".
So how can Wolfram pretend to claim that he has discovered this phenomenon? One key factor is that he either utterly misunderstands or utterly misrepresents the basics of chaos theory. Throughout the book, he equates chaos theory with the phenomenon of sensitive dependence on initial conditions (SDIC) and nothing else. Further he claims that any randomness that occurs in a chaotic system is purely a consequence of the randomness in the least significant digits of the initial condition (p149-155, p304-314).
Now, I wouldn't argue that SDIC is a key component of chaos theory, but it is not the only component. Selecting half a dozen books on chaos theory does give half a dozen slightly different definitions of chaos, but in none of them is SDIC given as the entire definition.
Now we turn to Wolfram's claim that all randomness in a chaotic system is produced from the fine detail of the initial condition (essentially, claiming that every chaotic system is just an instance of the shift map). Consider any dissipative chaotic system (such as the Lorenz equations, or the Rössler attractor). Because the system is dissipative, this means that all details of the initial condition are lost in the long time limit—and yet the long time behavior is still chaotic and random-seeming.
So where is the randomness coming from, if not from the initial conditions? Essentially, the underlying geometry of the nonlinear equations generates a strange attractor as the limiting behavior of the system, which is of zero measure and which has a fractal structure. This geometrically fractal structure in turn generates the apparently random dynamical behavior.
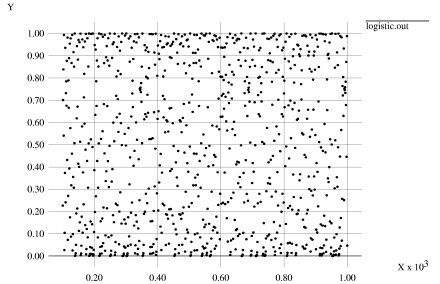
To take a simple example, consider iterations of the logistic map at a=4, starting from an initial condition of 1/8=0.125. This initial condition clearly does not have any randomness built into the initial condition (as it is a rational). But if we iterate this initial condition, we nonetheless see random-looking, chaotic behavior:

It might be plausible that the erratic behavior seen is just an artefact of the numerical iteration scheme used, with rounding errors being magnified at each iteration. However, the logistic map at a=4 has an analytical solution (which Wolfram gives on p1098)—and so no iteration was involved in generating this diagram.
So netting all of this down, Wolfram's randomness and complex structured behavior in cellular automata seem like just another example of a nonlinear chaotic system, albeit one that is easier to simulate than a fully-fledged numerical system.
Throughout the book, Wolfram raises concerns about the ubiquity of mathematical descriptions of systems.
Mathematics is useful precisely because it allows large scale summarization of a system, in a manner which may admit prediction of the behavior of that system. This is why mathematics goes hand in hand with science, for the key hallmark of science is that it yields verifiable predictions, and mathematical models allow this.
Wolfram attempts to replace the summarization of a system with a differential equation, with a more vague summarization of a system as a simple iterated rule. However, he himself admits that these rules do not admit prediction of their behavior in advance—other than just by running them.
This not to say that descriptive science is completely worthless; however, it is definitely a second class citizen behind predictive science (a quote from Rutherford about this distinction: "All science is either physics or stamp collecting").
p849, "Writing Style": Wolfram is right, starting sentences and paragraphs with conjunctions is indeed annoying.
p849, "Clarity and modesty": This paragraph is confusing personal modesty with modesty of ideas. If Wolfram believes that a particular idea is of huge import, then I have no problems with him expressing it so. However, I have concerns about his implicit claims that all of the ideas are his own personal invention—which they are not, or even close to.
p851, "Using color": Wolfram makes the startling claim that "it is easier to assimilate detailed pictures if they are just in black and white". While it is true that using different colors to present a continuous ordering is often misleading (see for example p153-154 of Tufte [1983]), there is plenty of evidence that using color to distinguish distinct features is very useful (see for example p52-54 of Tufte [1990]).
p852-853, "Notation": Personally, I find it extremely annoying that Wolfram refuses to use standard mathematical notation when he is describing standard mathematical systems. Much as I like Mathematica, there is no way I can justify the huge price involved in owning a copy now that I am no longer a student or an academic.
p860, "The Role of Logic": Logic was mostly famously viewed as a possible representation of human thought by Boole; however, it was viewed somewhat differently even by the late 1800s. For example, although the title of Frege's Begriffsschrift refers to "pure thought", in its very first paragraph:"we can inquire, on the one hand, how we have gradually arrived at a given proposition and, on the other, how we can finally provide it with the most secure foundation [...] the second is more definite".
p7, paragraph 2: The book does not really show a "vast range" of abstract systems that have not been considered before; it actually concentrates on one particular class of abstract systems, and some members of this class have already been studied (for example, Turing machines (p78), substitution systems (p82), register machines (p97) have all been studied, and the whole class has points in common with iterated difference equations). It is fair to say that Wolfram comes at these systems from a different direction than existing work, though.
p13, "Chaos Theory": This section only describes a single aspect of what chaos theory is about.
p14-15, "Experimental Mathematics": There are lots of "exceptions" to Wolfram's claim that only systems that have already been investigated by other mathematical means have been subject to experimental mathematics. The whole fields of cellular automata, genetic algorithms, neural networks, simulated evolution have all made use of experimental mathematics on previously little examined problems.
p15, "Fractal Geometry": I find this description of fractal geometry slightly misleading; the word "nested" implies a regularity about the detail found when you change scale. However, fractal geometry is commonly applied to shapes that have no such regular structure (for example, the coastline of Britain—see page 1 of Mandelbrot [1982]).
p15, "Nonlinear Dynamics": Nonlinear dynamics covers an awful lot more than just soliton theory, including bifurcation theory, limit behavior classification, symbolic dynamics, routes to chaos, time series analysis, etc. See Guckenheimer & Holmes [1983], Drazin [1992], Temam [1988].
p25-26: It's a shame that Wolfram relegates the correct name (Sierpinski gasket, see p.142 of Mandelbrot [1982]) for this shape to the notes (p.870)
p865, right hand column: Wolfram clearly doesn't keep up to date on his knowledge of the C language—his CA program is written in a pre-ANSI style (with Algol-like function declarations, see e.g. p239 of Harbison & Steele [1991]) that was deprecated in 1989 (and is not valid as a C++ program).
p57: Netting down the classification that Wolfram describes, I think the set of 256 possible behaviors is as follows.
p65, last paragraph: Personally, I would dispute that the "vast range" of systems that Wolfram presents in this chapter are all "utterly different".
p889, "History": I find Wolfram's claim that "in almost no cases has the explicit behavior of simple Turing machines been considered" a little odd, given that he goes on to reference some work in this area. I guess the applications to the halting problem don't count as "explicit" behavior.
p95, paragraph 1: "in some ways even simpler" (example of general theme).
p101, paragraph 6: Adding extra instructions "rarely seems" to have much effect (example of general theme).
p106, paragraphs 2 and 3: Modulo the "typically" and "usually", this claim hugely depends on your definition of "complex". Considering register machines or Turing machines, as their sizes get larger they support more advanced programs—for example, a program to produce prime numbers using the Sieve of Eratosthenes. Is this considered more complex behavior than the interactions of a rule 110 automaton?
p897, "Long halting times": Wolfram's suspicion that there are substitution systems that cannot be proved to reach a fixed point sounds very analogous to the Halting Problem or Gödel's Incompleteness Theorem to me.
p898, "History", second para: "among programming languages Mathematica is almost unique in also having the same feature" that there are no restrictions associated with types. I'm not sure I've understood this correctly, as all of the dynamically typed and functional languages have the same feature (for example, anything in the Lisp family - see Steele [1990] chapter 2).
p898, last sentence: "few truly meaningful computer experiments have ended up ever being done". Utter nonsense. From fractal geometry to chaos theory to artifical life to game theory, lots of computer experiments have been done. If these experiments are not "meaningful", then neither is anything that Wolfram has done.
p899, "History of experimental mathematics", last sentence: Claiming that he is exploring systems that have "never in the past been considered in any way" seems a little odd, given that the notes for this section contain a lot of references to existing work on the systems that he mentions (e.g. p893, p889, p894, p895)
p124, last paragraph: If the operation of addition is broken down into its individual steps, then the carry digits only have local effect at each step—so that a single numerical operation can correspond to just a collection of several CA steps. In this case, I suppose it is unsurprising that numerical systems do not display different behavior from CAs.
p143, penultimate paragraph: "At some level, one can always use symbolic expressions [..] to represent numbers". Incorrect. Counterexample: Chaitin's halting probability Ω cannot be expressed as a symbolic expression (see also p1067).
p919, first paragraph: "typically studies have concentrated on repetition, nesting and sensitive dependence on initial conditions—not on more general issues of complexity". What more general issues of complexity is he referring to? It's hard to think of a simple system that has been more comprehensively studied than iterated maps.
p919, "Problems with computer experiments": It is important to be clear that these problems are known about, and there are ways of addressing them.
p920, paragraph 4: "such randomness cannot in fact be a consequence of the chaos phenomenon". Wrong.
p152, paragraph 4: (Example of general theme.)
p153, paragraph 2: (Example of general theme.)
p161: Wolfram neglects to point out that one of the key ways that partial differential equations are derived is by considering the system as a collection of granular cells, and then calculating the limiting behavior as the cells get smaller (see, for example, the derivation (chapter 6 of Acheson [1990]) of the Navier-Stokes equations in fluid dynamics). This is roughly the same as cellular automata, but the summarization process has the advantage that predictions can be made
p162, paragraph 1: "as we shall see later in the book, it is certainly not that nature fundamentally follows these abstractions [PDEs]". I eagerly await his evidence for this statement.
p162, paragraph 8: Wolfram's "almost all" and "at least in one dimension" caveats are not enough to save this statement from absurdity. He himself gives three more examples in the notes (p925), and there are others (such as the Ginzburg-Landau equation, of which his nonlinear Schrödinger equation is a special case, or the Korteweg-de Vries equation).
p164, last paragraph: Wolfram makes my point for me, that chaos and randomness is already known to occur in partial differential equations.
p 923, "Existence and uniqueness": "PDEs do not have a built-in notion of 'evolution' or 'time'". Except of course for the large classes of PDEs that are normally referred to as "dynamical systems" or, er, "evolution equations".
p167, paragraph 5: While it is true that there has been a lot of unwise trust in numerical approximations, a serious scientific approach will involve cross-checking a variety of different numerical schemes and gridsizes to ensure that any artifacts are in the system not the numerics, together with theoretical tests.
p924, "Numerical Analysis": Wolfram himself illustrates that the problem of instability in numerical solution of PDEs is well-known and susceptible to analysis, but nevertheless continues to imply that work in this area does not or cannot distinguish between numerical behavior and system behavior.
p924, right hand column, paragraph 2: There are plenty of publications which show highly complex behavior in PDEs.
p189/p932, "Dragon curve": This is referred to as the Harter-Heightway Dragon in Mandelbrot [1982] (p66), although Wolfram gives no attribution.
p189, last paragraph: "building up patterns by repeatedly applying geometrical rules is at the heart of so-called fractal geometry". Not true. Famous counterexamples: the Mandelbrot set, or the coastline of Britain. Rule-based fractals are used a lot to illustrate basics of the real heart of fractal geometry, which is the study of curves that are self-similar at different scales (and which have a non-integer Hausdorff Besicovitch dimension)—and this key idea applies both to rule-generated fractals and to fractals encountered in dynamical systems or in real-world systems. I shall pass over the insulting use of the word "so-called".
p190, last paragraph: Again, I dispute Wolfram's claim that "traditional" fractal geometry only studies patterns that have a purely nested form. There can be no more "traditional" reference for fractal geometry than Mandelbrot [1982], and fractals that do not have a pure nested form definitely appear therein (chapters 5, 9, 10, 11, 13, 14, 15, 16, 19, 20, 21, 23, 24, 25, 27, 28, 32, 34, 35, 36, and 37 all consider fractal behavior that is not purely nested, in some form).
p194-195: On my copy of the book, the arrows in the figures on these pages are pretty much invisible.
p221, last paragraph: "traditional science and mathematics [have a] failure to identify the fundamental phenomenon of complexity". I completely disagree.
p261, paragraph 1: A somewhat obvious rhetorical question, given that Wolfram has already demonstrated random behavior from a single black cell initial condition.
p262, paragraph 2: This paragraph applies equally well to chaotic systems, particularly in dissipative systems when initial transients are removed.
p955, "Sarkovskii's theorem": This section provides a perfect example
of Mathematica notation being much less
clear than standard mathematical notation. Compare Wolfram's
formulation with the standard formulation (see Sarkovskii [1964] or section 1.10 of Devaney
[1989]):
Wolfram: if a period m is possible then so must all
periods n for which p={m,n} satisfies
OrderedQ[(Transpose[If[MemberQ[p/#,1], Map[Reverse,
{p/#,#}],{#,p/#}]]&)[2^IntegerExponent[p,2]]]
Devaney: if a period m is possible in the ordering
below, then so must all periods n later in the ordering
3>5>7>9>...>2.3>2.5>2.7>...>22.3>22.5>...
>23.3>23.5>...>23>22>2>1
p959, "2D generalizations": I cannot find the discussion at the end of Chapter 5 that Wolfram refers to, and the index has no entry for entropy in that chapter.
p961, "Attractors in systems based on numbers": Minor clarification: the term "limit cycle" usually refers to a purely periodic orbit, in which case the quasiperiodic cycle (a cycle with two irrationally related periods, which fills out a torus) needs to be added to the list of possible attractors.
p961, "Attractors in systems based on numbers": "the structure of the [strange] attractor is almost invariably quite simple". Even allowing for the "almost" and lack of definition of "simple", I'd disagree that (say) the Lorenz attractor or the Rössler attractor qualify as simple.
p297, paragraph 2:"One of the main discoveries of this book" is misleading. There is lots of background to this discovery; a more accurate statement might be "One of the main observations presented in this book".
p298, paragraphs 1-4: This seems extremely vague to me. It boils down to "these things look the same, therefore they are the same", with no evidence presented.
p298, paragraph 6: "it suggests that the basic mechanisms responsible for phenomena that we see in nature are somehow the same as those responsible for phenomena that we see in simple programs". Suggests, maybe, but that's not really strong enough to be anything other than a passing observation.
p299, figure caption: (Example of general theme.)
p968, paragraph 1: "it has normally been assumed that [..] realistically complicated behavior can only ever be obtained if explicit randomness is continually introduced". Complete nonsense.
p304, "Chaos Theory and Randomness from Initial Conditions": Frankly, Wolfram's understanding of chaos theory seems to have come from watching Jurassic Park (Example of general theme.)
p309, paragraph 3: Wolfram comes close to getting a clue here, and realising that sensitive dependence on initial conditions is not the entire definition of chaos.
p309, paragraph 5: I should like to see references for this assertion that accounts of chaos theory are confused over the introduction of randomness in initial conditions.
p309, paragraph 5: I don't understand what the problem is with this implicit assumption that "random digit sequences should be almost inevitable among the numbers that occur in practice". Irrational, and indeed normal, numbers are dense among the real numbers, and so it would be surprising if non-random digit sequences turned up in initial conditions.
p972, paragraph 1: As a one-time chaos theory specialist, I would disagree with Wolfram's claim that Gleick's book "covers somewhat more than is usually considered chaos theory". I am also at a loss to find where the book mentions Wolfram's work on cellular automata, as he and they are not included in the index.
p972, "Recognizing chaos": (Example of general theme.)
p322, paragraphs 3-6: Wolfram's discussion of mechanism "producing new randomness" in "a much shorter time" and in a way which is "more efficient" is maddenly unquantifiable.
p329, paragraph 1: Note that the Central Limit Theorem applies much more generally than just to random walks. (see e.g. chapter 8 of Grimmett & Welsh [1986]).
p337, last paragraph: That continuous changes can induce non-continuous results is the key observation of catastrophe theory, which sprang to prominence in the early 1970s.
p342, paragraph 4: "to work out what pattern of behavior will satisfy a given constraint usually seems far too difficult for it to be something that happens routinely in nature". Leaving aside the "usually seems" weasel words, this is a statement that is extremely difficult to justify. Just because it is difficult to program a computer to act in accordance with a physical constraint does not mean that the corresponding physical system has any such difficulty. For example, consider water standing in a complex system of pipes. It may be very difficult to calculate exactly where the water will level off and prove that all of the pipes will have the water at the same level—but the water itself has no such problem of calculation. (Part of this disagreement may be due to the limited forms of constraint that Wolfram considers).
p348, paragraph 4: "often" would be more accurately read as "sometimes".
p351, paragraph 2: The amount of prevarication in this paragraph is remarkable: "so far as I can tell", "more or less", "most plausible", "tends". I'd still disagree; there are a vast number of systems which are usefully expressed in terms of constraints, particularly action principles.
p351, paragraph 3/p985, "Biologically motivated schemes": It is not really the case that natural selection is optimizing for some aspect of form of behavior, or that is constraint based. Natural selection optimizes fitness, which is in turn driven by the environment of the organism and also the current fitness of all of the other organisms in that environment.
p351, last sentence: (Example of general theme.)
p354-355: This classification of behavior is essentially the same as the classification of possible limit behaviors of ordinary differential equations (see p961).
p356, last paragraph: I remain unconvinced that constraints are "rarely a good explanation for actual repetition that we see in nature".
p357, last paragraph: "to get nesting seems to require that there also be some type of discrete splitting or branching process". This depends on Wolfram's definition of "nested", which appears to change throughout the book. If "nested" just means fractal, then this statement is wrong—there are many fractals which are not formed from any branching process. If "nested" means those specific fractals that are formed by a substitution or branching process, then this specific statement is true (but many other statements throughout the book are then overly restrictive).
p358, paragraph 2: "as we have discovered in this book". Misleading—this implies that Wolfram himself has discovered this, which is of course nonsense.
p359, top diagram: Given that time evolution is running down the page, I would disagree that this cellular automata is generating nesting—quite the reverse!
p360, paragraph 5: "nesting cannot be forced [..] forced fairly easily by constraints". I disagree. Many differential equations are generated by considering constraints, and in turn these differential equations can often have fractal strange attractors.
p989, "Self-organized criticality", first sentence: Mandelbrot's work in the late 1970s already indicated that nesting does not need fine tuning of parameters.
p990, "Structure of algorithms": "until recently even recursion was usually considered rather difficult". This will come as a surprise to the large number of people who have been working with functional languages for the last forty years.
p990, "Structure of algorithms": "no doubt the methods of this book will lead to all sorts of algorithms". Personally, I can't see very many potential algorithms arising from cellular automata, as they don't normally solve problems.
p363, paragraph 2: "rather little turns out to be known" is a very strong statement, and I personally don't feel that it is justified by the contents of the chapter (particularly when the information in the notes is bourne in mind).
p364, paragraphs 2-3: (Example of general theme.)
p364, paragraphs 5-6: Wolfram's description of the process of science is a misrepresentation. It is true that experiment is often only compared with the models for a few variables, but Wolfram neglects to point out that these variables are typically sampled many, many times to obtain a time series which can be compared against the continuous behavior of the model. This procedure has considerable mathematical justification.
p991, "Models versus experiments": It's hardly news that experimentalists get it wrong sometimes.
p367-268: I would be interested to see examples of the process of model complication then simplification that Wolfram describes.
p368, paragraph 3: (Example of general theme.)
p369, paragraph 1: If, as Wolfram claims, numerical models do not necessarily match the mathematical models that in turn may not match the real system, then similar concerns must also apply to a cellular automata model that has no physical justification other than "it looks right". Surely the best approach is to use the right model for the job—if the underlying processes seem to be discrete and local, then a cellular automata model is appropriate; if the underlying processes involve more global interactions, and continuous ranges of behavior, then a mathematical model is more likely to be appropriate.
p370, last paragraph: Aha, a verifiable prediction.
p371, last paragraph and p372 paragraphs 4-5: Given that Wolfram claims his CA models get the basic features of snowflake generation right, it would interesting to see how these models would do if more of the complicating issues were included.
p373, last paragraph: A verifiable prediction.
p992, "Identical snowflakes": Interesting. How does the six-fold symmetry turn up (presumably from the underlying ice crystal lattice structure) and get preserved during snowflake formation? Does make it sound like diffusion-limited aggregation (DLA) models are less convincing.
p375: An interesting model, although possibly a little too descriptive to yield verifiable predictions.
p376, paragraph 6: One of the key observations of chaos theory was that nonlinear equations can generate random-seeming behavior; as such, the development of chaos theory made it much more plausible that turbulent flow could be a consequence of the nonlinearity of the Navier-Stokes equations.
p997, "Navier-Stokes equations": While it is true that numerical integrations of the Navier-Stokes equations need to be considered with some caution, it is a little harsh to claim that it is "almost impossible" to distinguish between numerical artifacts and mathematical artifacts (for example, one can use radically different numerical approaches and compare their results—if they have the same features, it is unlikely to be a consequence of numerical artifacts).
p999, "History of cellular automaton fluids": As Leo Kadanoff points out, Wolfram neglects to mention earlier work than his own, and also later work that surpasses his own.
p377-378: The cellular automata model that Wolfram describes here is essentially the same as how the Navier-Stokes equations are derived. (cf. chapter 6 of Acheson [1990]).
p381, paragraph 1: (Example of general theme.)
p381, paragraph 2: Wolfram claims that none of the chaotic equations derived from fluid dynamics "have any close connection to realistic descriptions of fluid flow". This would come as a bit of a surprise to some.
p382, paragraph 2: Simulation of randomness generation does not need a new cellular automata model; the nonlinear Navier-Stokes equations are quite capable of generating randomness themselves.
p382, paragraph 3: The diagram does not look "strikingly similar" to turbulent fluid flow to me.
p382, paragraph 7: Personally, I would predict that "remarkably simple programs" that "successfully manage to reproduce the main features of even the most intricate and apparently random forms of fluid flow" will turn out to be . . . numerical integration programs for the Navier-Stokes equations.
p998, paragraph 3: As Wolfram points out, in a dissipative system the details of the initial conditions will indeed be damped out—but still chaotic behavior is observed. He nearly gets the point, but not quite.
p998, right hand column: Wolfram claims that his CA model of fluid flow is "seems to provide essentially the first reliable global results". Leaving aside the weasel words "seems", "essentially", this is a strong (and unlikely) claim.
p1000, paragraph 1: Amusing hissy fit. I wonder to whom he refers here?
p1000, "Generalizations of fluid flow": It is also straightforward to generalize the Navier-Stokes equations to these situations.
p383, paragraph 5: I enjoy the hubris of Wolfram pointing out that the genetic code for building a human being is just about "as complex as" his own particular software project, Mathematica. I've not seen any evidence of Mathematica producing philosophy, symphonies or new physics yet.
p386-387: I disagree with Wolfram's over-simple characterization of evolution as producing optimal solutions to environmental problems. I think it's quite well known that it merely produces solutions that are more optimal than the others that happened to be around at the same time.
p388, paragraph 6: I'm not convinced that traditional biological thinking does assume that all complexity in organisms is "carefully crafted to satisfy some elaborate set of constraints", as Wolfram claims (witness the Dawkins-Gould debate on essentially this point).
p1002, "Tricks in evolution": Probably also worth mentioning co-evolution and more general arms races.
p392, paragraph 1: "natural selection can only operate in a meaningful way on systems whose behavior is in some sense quite simple". No evidence given for this statement.
p392, paragraph 4: "with more complex behavior [..] it becomes infeasible for any significant fraction of these variations to be explored". a) No-one is claiming that all of the potential variations have been explored b) complex adaptations can be built up by accretions of simpler adaptations.
p394, paragraph 3: "if natural selection is to be successful [..] it seems what is needed are components that behave in simple and somewhat independent ways". Wolfram presents no evidence for this claim, and besides there are many biological systems that have evolved with extremely complex interlinked components (for example the ATP chain).
p396, paragraphs 4-5: These paragraphs depend hugely on what your definition of "complexity" is. If you count sophistication of function (e.g. the eye) as complexity, then there is no problem with natural selection producing complexity. If, on the other hand, you take complexity to mean complicated, random-seeming patterns (e.g. pigmentation), then yes it is difficult for evolution to produce any specific pattern directly (because the information content is so high but the effect on fitness is so low).
p397, paragraph 5: Rather than suggesting that it "might be possible to develop a rather general predictive theory", this section would be more convincing if it actually did present a predictive theory. As it stands, what Wolfram has described seems to only apply to a small area of biological development (texture, pigmentation and branching patterns, essentially).
p398, paragraph 6: Wolfram repeats his flawed assumption that evolutionary theory requires adaptations to be globally optimal.
p397, paragraphs 7-8: These paragraphs again depend on the meaning of the word complexity.
p1005, "History of branching models", last sentence: "nothing like the simple model that I describe in the main text has ever been considered before". Apart from all of the examples that he's just given, presumably?
p404, paragraph 6: Again, I disagree with the assertion that this is a universal belief among biologists.
p410: Note that Wolfram points out (p1007, "History of phyllotaxis"), that this is not a new model for budding.
p422, paragraph 2: I disagree with the claim that Wolfram has shown what is needed to product the "kind of diversity and complexity we see in plants and animals". He has shown what is needed to produce some specific aspects—budding, branching, pigmentation patterns—but no sign of a general theory that could explain (for example) why animals heads are on the tops of their bodies, why plants grow upwards, why quadrupeds are common. The theory of evolution by natural selection is such a theory—particularly when it is appreciated that evolution does not necessarily produce the most optimal organisms.
p422, paragraph 3: Whether a particular underlying set of CA-like rules for a biological feature is "picked almost at random" is surely going to depend on the fitness characteristics of that feature. If twenty different CA rules for pigmentation all produce the same level of camoflage, then yes the choice will be at random. If ten rules produce significantly less effective camoflage patterns, then those rules will not be among those selected at random. Another example would be CA rule for plant branching patterns—any rules that generated less efficient leaf shapes would be selected against.
p431, paragraphs 3-4: With its equivalent characteristic of randomness generation, chaos theory has also been considered as a likely candidate for the generation of financial randomness.
p434, paragraph 2: I disagree that the origins of the Second Law of Thermodynamics are quite as "mysterious" as Wolfram claims. Indeed, Wolfram himself admits (p1020) that the "clear understanding" he claims to bring is actually very similar to the standard explanation.
p434, paragraph 4: Not a new discovery.
p434, last paragraph: "There is still some distance to go" before Wolfram solves the most fundamental problem of physics. I couldn't agree more.
p1018, "History": If you read between the lines, the notes for this chapter do indicate just how much of the thinking in the chapter and indeed the entire book are closely related to earlier work by Edward Fredkin and Tommaso Toffoli, [10-Apr-02] and Konrad Zuse before that.
p1018, "Emergence of reversibility": I don't follow what Wolfram means by "approximate reversibility", and his reference to p959 doesn't help either.
p442, paragraph 1: (Example of general theme.)
p444: Wolfram's explanation of the emergence of the Second Law of Thermodynamics based on the initial conditions being somehow special is essentially equivalent to the explanation given in chapter 9 of Hawking [1988], or that in chapter 7 of Penrose [1989]
p445, paragraph 1: Although Wolfram does do a good job of elucidating how it is that irreversible behavior in the large can develop from reversible rules in the small (based on special initial conditions), I disagree that this has been "until now [..] rather mysterious".
p1020, "My explanation of the Second Law": Wolfram admits here that what he says "is not incompatible with much of what has been said about the Second Law before", which belies his repeated claims to have solved what was previously completely mysterious.
p1021, "Cosmology and the Second Law": I don't understand the statement that "the effective rules for the evolution of matter led to rapid randomization, whereas those for gravity did not". Unless he has some claim to have displaced general relativity, surely the distributions of mass and of gravity are inextricably interlinked?
p1021, "Alignment of time in the universe": Wolfram is claiming here that the direction of thermodynamic arrow of time is induced by the the direction of the cosmological arrow of time, to use the terminology of Hawking [1988], although he offers no rationale (such as the weak anthropic principle) for this.
p451, paragraph 1: (Example of general theme.)
p453, paragraph 4: I'm not sure why Wolfram apparently believes it so surprising that a completely invented computer simulation should not obey the Second Law of Thermodynamics.
p453, paragraph 6: The argument that biological systems apparently disobey the Second Law of Thermodynamics is common among creationists and as such has been comprehensively argued against.
p455, paragraphs 3-5: Wolfram is skipping a step in his argument here, as he simply equates the radiation of information from his CA system with the physical radiation in the universe. Nevertheless, the argument appears to be a restating of the usual rule of thumb that whenever the Second Law appears to be violated, it is typically because you are not considering a closed system in its entirety.
p457, last paragraph: Wolfram "strongly suspects that there are many systems in nature" which behave like his constructed experiment in not following the Second Law—but does not give a single (even tentative) example to back up his intuition.
p1023, PDEs: Relevant references for this: section 5.1 of Drazin & Johnson [1989], section 1.6 of Ablowitz & Clarkson [1991], section 7.3 of Olver [1986]
p464, paragraph 1: Note sure why Wolfram considers it "striking" that the average density of a system made up of discrete cells should behave continuously.
p464, last paragraph: "One might have though that continuum behavior would somehow rely on special features of actual systems in physics." Or not, in fact.
p1024, "Derivation of the diffusion equation": Note that there appears to be an additional assumption not explicitly mentioned in this derivation, of an underlying left-right symmetry in the underlying CA.
p465, paragraph 3: (Example of general theme.)
p465, paragraph 6: This is not, in fact, a new idea—it has certainly been around long enough to make an appearance as a backdrop to science fiction (for example, Greg Egan's Permutation City).
p466, paragraph 5: Of course, if the complete behavior of the system is known, rather than just the "overall features", then it is fairly trivial to recreate the the underlying rules.
p468, paragraph 5: Is there any evidence that The Rule for the universe will be simple, other than that Wolfram has a hunch and that (p470) existing laws of physics tend to favour simple formulations?
p1025, "Theological Implications": Wolfram makes the claim that a universe with an underlying rule makes it impossible to have miracles or divine intervention. This seems a strange claim, for even in his simple CA systems it is entirely possible for Wolfram to stop the evolution and alter particular cells, and then let the evolution continue from that point—which would appear exactly as a miracle to any putative inhabitants of the CA universe.
p1025, "Simplicity of Scientific Models": At last, an admission that a majority of complicated features in biology are due to the vagaries of biological evolution, not CA-like rules.
p1026, "The Anthropic Principle": Wolfram is making the astonishing claim that his little pictures of interacting structures in cellular automata are "ultimately not dissimilar to intelligence". Their complexity is nothing like intelligence; even allowing for the fact that CA models can support universal computation, this is a long way from demonstrating intelligence—as forty years of ultimately unsuccessful research in artificial intelligence has shown.
[10-Apr-03] p1026, "Mechanistic Models": Zuse [1967] appears to be the earliest reference for the "all is computation" approach that Wolfram claims is his (although I've only looked at Zuse [1969], since I don't read German). Thanks to Jürgen Schmidhuber for pointing out this earlier reference to me.
p1026, "Mechanistic Models": The name Edward Fredkin is coming up again...
p473, paragraph 5: Wolfram seems to be arguing here that because he has gotten used to his particular form of models, that the universe should follow suit.
p474, last paragraph: Wolfram claims that programs with discrete elements make it "much easier for highly complex behavior to emerge". Not so.
p1027, "History of discrete space": The name Edward Fredkin is coming up again...
p1029, left column, last two lines: Wolfram is actually referring to cubic or 3-regular graphs not just trivalent graphs here.
[04-Mar-03] p475 onwards: This potential description of space as being generated by an underlying evolution of a graph network shares some similarities with Regge calculus and Superspace; see chapters 42-44 of Misner, Thorne & Wheeler [1973]
p481, paragraph 2: Wolfram claims that "space and time somehow work fundamentally the same" in modern models of fundamental physics. I'm not convinced that this is an accurate characterization.
p482, paragraph 4: As in chapter 5, why is it relevant that it is difficult to compute constraint-based systems? Isn't this assuming the result that Wolfram is trying to prove, namely that physics is generated from computation?
p482-484: Wolfram is arguing a general position from a very specific limited definition of constraints. Many differential equations are constraint based and nevertheless have well established proofs of the existence of unique solutions given suitable boundary conditions or initial conditions.
p484, paragraph 5: I still disagree with this characterization.
p486, paragraph 1: Wolfram seems to claim here that time and space symmetry will emerge from The Underlying Rule, without indicating how this will come about.
p486, paragraph 4: I don't understand why it "seems unreasonable" for all of the cells of The Underlying Rule to update simultaneously; presumably his intuition is driven by present day implementation of CAs on serial hardware, which is somewhat limiting.
[14-Apr-03] p486, last paragraph: Wolfram suggests that the universe might actually be "like a mobile automaton or Turing machine". This has also previously been suggested in Schmidhuber [1997].
p504, paragraph 2: I don't understand why this property is "remarkable"; it's just a logical consequence of the structure of the underlying rule.
p505, paragraph 4: I find Wolfram's analogy between historical belief that the Earth was the centre of the universe and the current belief that we have a unique history to be dubious at best.
p506, paragraph 2: (Example of general theme.)
p511: In my copy of the book, the clocks are pretty much illegible in this diagram.
p515, last paragraph: I don't follow why this randomness in proposed underlying network should allow a dimensionality of 3 to emerge.
p1038, "Random replacements": I believe rule T1 adds one edge to two faces, not two edges to one face—and similarly removes one edge from two others.
p1038, "Random replacements": The average number of edges must only remain at 6 because it is preserved from the (hexagonal) initial condition; a different initial condition would presumably have a different average.
p517, paragraph 2: It's worth being clear here (and elsewhere in the chapter) that Wolfram is assuming that all of his earlier suppositions are indeed true.
p520-522: Interesting suggestion.
p524: I disagree with Wolfram's claim that his presentation of relativistic time dilation is "considerably clearer" than other accounts. Personally, I found his diagram fairly impenetrable (but I consider myself a mathematician and so prefer more standard presentations—for example in Schutz [1985])
p1042, "Inferences from relativity": Wolfram appears to be claiming that because clocks in GPS satellites are corrected for time dilation, they no longer display time dilation. Just rescaling a clock is hardly a counterexample to the entire time dilation effect.
p525, paragraph 3: It would be very helpful in this chapter if Wolfram were to clearly distinguish between verified aspects of current physics, verifiable predictions about physics derived from his proposed new models, and random speculation. I presume his claim that it is "almost inevitable" that leptons have internal structure falls somewhere between the latter two camps.
p527, last paragraph: Again, Wolfram is ignoring a lot of pre-existing work. In the particular area of modern physics, it is also worth noting that before the invention of quark theories, the menagerie of apparently fundamental particles looked very complicated. But a simple underlying theory was found to explain the complication.
p527-529: An interesting approach. Sadly, I don't understand enough string theory to see if there are parallels between the two approaches.
p537, paragraph 2: I am startled by Wolfram's hubris in talking about the limitations in the Einstein equations, when his own model of physics is still a incomplete, vague, unverifiable suggestion.
p539, paragraph 2: (Example of general theme.)
p547, paragraph 1: No. We have not discussed "the basic mechanisms responsible" for various phenomena. We have instead discussed some potential rough models that might be related but have not yet been verified in any way.
p548, paragraph 1: The processes involved in perception and analysis are in fact studied in various areas of traditional science, such as neurology, psychology, cognitive science and quantum mechanics.
p548, paragraph 3: Again, quantum mechanics has definitely pushed the process of perception and analysis to the foreground in science.
p549, paragraphs 1-3: Compare algorithmic information theory.
p550, paragraph 4: (Example of general theme.)
p551, paragraph 2: "discovered in this book". No. Not true
p552, paragraph 2: Given that Wolfram claims that the concept of randomness has "remained quite obscure", I find it odd that he goes on to spend three pages attacking the standard concept of randomness...
p554, paragraph 3: (Example of general theme.)
p555, paragraph 2: There is already perfectly well-known terminology for sequences which appear to be random, but are generated from underlying rule systems: "pseudo-random".
p556, paragraph 3: This proposed definition of randomness does rather shift the conceptual difficulty from the word "random" to the word "simple".
p1068, lines 1-2: Given that statistics is the particular area that studies randomness, it seems harsh to attack fields outside of statistics for not being experts on randomness.
p557, paragraph 1: Personally, I felt that the book so far was hugely lacking of a coherent definition of complexity
p557, paragraph 2: I disagree with Wolfram's thesis that normal visual perception is all that we can do to identify complexity. Consider the sequence of primes above 1000; to the naked eye they would appear fairly random (except perhaps that there are no even numbers). However, with a little intellectual analysis it could be discovered that they were structured in a very particular way.
p559, last paragraph: (Example of general theme.)
p567, paragraph 2: Wolfram is correct to point out that most compression schemes are 1D, but the particular approach that he goes on to describe is far from the only 2D compression algorithm. Examples include T.128, JPEG, MPEG, Barnsley's Iterated Function Systems.
p570, paragraph 1: MPEG-4 is an example that does use some similar schemes in practice.
p570, last paragraph: Barnsley's IFS approach may have better compression characteristics for nested image (see chapter 5 of Peitgen [1988]), although some controversy is involved.
p572, paragraph 1: I'd disagree that just because compression algorithms do not generate a huge reduction that this implies that the source is random.
p572: Aarg. Why can't Wolfram use the same terminology as the rest of the known world? The standard term is "lossy", not "irreversible".
p580, paragraph 2: It hardly seems surprising to me that perception systems based on essentially the same processes as those that generated the patterns should be able to distinguish between the patterns. To make his jump to the suggestion that this is actually how perception works, at least one of the two processes (generation, perception) should be based in the real world.
p582, paragraph 4: Note that this only applies to regular nested patterns; our visual systems may respond better to more real-world fractals.
p1075, right column, line 18: Claiming that there is "no doubt" about a statement that he presents with zero evidence is somewhat strong, even allowing for the "can be idealized" weasel words.
p588, paragraph 4, sentence 2: Absolutely not the case.
p588, paragraph 5: Comparing a model with observation is a rather more subtle process that Wolfram suggests, particular when the model is nonlinear and displays sensitive dependence on initial conditions.
p589-590: Wolfram is ignoring a common technique for checking models, which is to build the model from a subset of the available data, and then to test that the model produces results which are consistent with the remainder of the data.
p591, paragraph 2: It is very annoying that Wolfram does not provide page numbers for his reference back to chapter 5—that chapter is over 50 pages long.
p593, paragraph 3: Much as I concur with Wolfram's attack on many stochastic modelling approaches, I feel that this statement is a misrepresentation of their position. A weighted coin is still perfectly random, but does not have a flat probability spectrum.
p595 paragraph 2: Presumably the second mention should also be (e) and (f) rather than (d) and (e).
p1083, "Time series": Wolfram is far too quick to dismiss nonlinear time series analysis (possibly reflecting his peculiar ideas about chaos theory). To quote page 7 of Weigend & Gershenfeld [1994], describing the results of a time series analysis competition: "all of the successful entries were fundamentally nonlinear"
p598 onwards: Wolfram's insistence on expressing everything in the form of cellular automata gets annoying, particularly as it often obscures clear explanation. I guess that this is just part of his campaign to subconsciously persuade the reader round to his point of view.
p602, last paragraph: Again, this is not a new discovery in this book. It's also instructive to consider the example in pages 4-5 of Knuth [1981], where complicated rules yield simple behavior.
p606, paragraph 2: This system hardly qualifies as having survived a serious cryptanalytical attack. See also the comments on p414 of Schneier [1996]
p1086, paragraph 1: There are in fact a number of other cryptosystems that are not DES, LFSR or RSA, even if you count all block ciphers as equivalent to DES—for example, RC-4. See Schneier [1996] for more information.
p1089, "Problem-based cryptography": It is not true that cryptography systems are solely based on integer factorization. Firstly, symmetric algorithms typically have little to do with number theoretical problems. Secondly, there are counterexamples even in asymmetric cryptosystems: the Rabin algorithm involves square roots modulo a composite number; the ElGamal algorithm involves calculating logarithms under a field; the McEliece system involves the use of error-correcting Goppa codes.
p1090, paragraph 2: Another amusing piece of hubris: because Wolfram has studied rule 30 for some time he has confidence that it is as difficult as the problem of factoring integers—which has been studied by rather more people, for rather longer.
p607, paragraph 2: It should be noted that the "right approach" that Wolfram mentions goes back to Cantor.
p612, paragraph 4: The surprise that Wolfram mentions is considerably lessened when one realizes that the first fractals were explicitly constructed to be pathological counter-examples for mathematical analysis.
p620, last paragraph: (Example of general theme.)
p621-623: Wolfram's hashing scheme seems a more contrived treatment than the standard fact that neural networks can demonstrate a form of content-based addressing (which he sort of describes on pages 624-625).
p627, paragraph 3: It is hardly a surprise that logic is not an appropriate idealization of all of human thought. Again, the first paragraph of Frege [1879] illustrates this.
p627, paragraph 6: I disagree with the claim that Mathematica is somehow unique (as it is essential a Lisp-like system optimized for mathematics), and with the claim that Mathematica mimics the operation of human memory.
p1103, "Structure of Mathematica": The structure Wolfram describes is essentially the same for all Lisp-like languages such as Mathematica.
p628, paragraph 3: (Example of general theme.)
p628, paragraph 4: On one level this is obviously true, since human brains are built of neurons and it is known that neurons behave according to simple rules. One another level, this offers no explanation that covers the levels between neuronal activity and intelligence.
p629, paragraph 2: Although I agree with this characterization of many areas of artificial intelligence (see also chapter 4 of Hofstadter [1994]), there are exceptions—for example, the Copycat project and its descendents.
p629, paragraph 3: (Example of general theme.)
p630, paragraph 4: This claim does not match with the meta grammar approach of Chomsky (as presented for example in Pinker [1994], and mentioned by Wolfram on p1181). The generalization of grammatical rules in children is not arbitrary; it is constrained to instances of the universal metagrammar.
p630, paragraph 5: Wolfram claims that we can learn languages with almost any structure. However, there is no evidence of this; the range of known human languages far from exhausts the theoretical possibilities for language structures.
p1100, paragraph 1: I'm not sure that neural network proponents would agree with this characterization of their approaches as simply equivalent to continuous probabilistic models.
p1100, "Sleep": Does Wolfram have any evidence for this physiological claim, or is he simply making it up?
p1103, "Languages": Again, Wolfram overstates the claims of Mathematica versus its competition, in this case by not distinguishing between the core language and its standard libraries. Both C++ and Common Lisp have extensive standard libraries which make them at least as large as Mathematica. Both also support a variety of styles of programming—imperative, functional, object-oriented, generic—to an equivalently wide degree as Mathematica.
p1103, "Languages": The claim that computer languages are almost always designed by a single person is false (see Common Lisp, C++, Ada, ..), as is the claim that they are designed once and for all (see Common Lisp, C++, Perl, ..)
p1103, last paragraph: I was under the impression that more universal features than just nouns and verbs had been discovered in human languages.
p1104, "Game theory": Wolfram denigrates the discoveries regarding the evolution of cooperation as a "folk theorem", but neglects to offer any criticism or counter-examples.
p632, paragraph 3: (Example of general theme.)
p634, paragraph 4: There are definitely examples where we get much further than our own built-in powers of perception take us. As well as my hypothetical example above, any successful cryptanalysis attack would count, as would the discovery of high-dimensional correlations in pseudo-random number generators (see p320).
p634, last paragraph: As mentioned elsewhere, this is a significant misrepresentation of evolution theory.
p637, paragraphs 2 and 4: I disagree that mathematical analysis is only useful when behavior appears simple; Wolfram has just hand-picked particular examples in chapter 10 to give this impression. One particular example that I happen to know about: the route to chaos in a homoclinic system, which displays much complex behavior that is nevertheless susceptible to analysis.
p1108, "Practical computers": An excellent reference for understanding the internal workings of computers is Tanenbaum [1984].
p643, paragraph 5: Universal systems cannot produce arbitrarily complex behavior; for example, none of them can compute the halting probability Ω.
p644, paragraph 3: It only seems implausible that cellular automata could be universal systems if you are unaware of the sketch proof of universality in the Game of Life automata, from the 1970s, and indeed of the very earliest CAs generated by von Neumann with the exact intent of being universal (see p1117)
p644, paragraph 5: (Example of general theme.)
p674, paragraph 3: It is indeed a remarkable result that all of the systems that Wolfram mentions can emulate each other, but it has been known about for quite some time. That is, it has not been "discovered" in this book, as Wolfram makes clear in the various "History" sections in the notes to this chapter.
p678, paragraph 3: It is worth being clear that the "several years of work" was not actually Wolfram's work.
[31-Oct-02] p1117, Totalistic rules: It's not clear whether Wolfram is claiming that his examples are actually universal, or just candidates for universality. See Gordon [1987] for an explicit example of a universal, totalistic, 1-D CA.
p675-689: I realize that Wolfram consistently refuses to acknowledge anyone other than himself in the main text, but it nevertheless seems particularly churlish in this case—where he is presenting 15 pages of someone else's work in detail.
General: Wolfram seems willing to give explicit page references in some instances in this chapter (p682 paragraph 5, p689 last paragraph, p695 paragraph 1) but not in other places. Some correlation with the strength of the argument that he is referring to, perhaps?
p1122, line 3: Note that the term "currying" is named after Haskell Curry.
p719, last paragraph: As Wolfram points out on the next page, it is hardly the Principle of Computational Equivalence that would break one's assumption that different systems would have different computing capabilities. This is just a consequence of the well-known phenomenon of universality.
p1125, "Basic framework": The "all is computation" approach is hardly unique to Wolfram.
p720, paragraph 7: Personally, I feel that the number of successes among the models that Wolfram presents are actually quite sparse—shell shapes, pigmentation patterns and his rehash of fluid dynamics. The others hardly qualify as successful models, as they are too vague, too untested and too untestable.
p720, last paragraph: I suspect Roger Penrose would disagree with this claim that there is no uncomputable physics (see chapter 10 of Penrose [1989]).
p726: I must admit that I find Wolfram's wording of the Principle of Computational Equivalence less than clear. It took me a couple of readings to figure out that the "equivalent sophistication" is an equivalence across the entire class, to a universal Turing machine.
p726, paragraph 5: I disagree that the Principle has "vastly richer implications" than other laws in science. There are few direct implications presented, and the indirect implication that there may be computationally irreducible processes in nature is hardly a rich seam for science.
p727, paragraph 5: To put this paragraph another way: the Principle of Computational Equivalent is unfalsifiable.
p728, paragraph 4: I dispute the claim that he has modelled a "wide range" of systems.
p728, last paragraph: Again, Wolfram's limited concept of constraints and the need to compute solutions to them comes into play.
p729, paragraph 3: This is misleading; Wolfram is not distinguishing between local and global minimization. As for evolution, biochemists are unlikely to claim that every molecule has to be in a global minimum energy.
p726, paragraph 6: This is not evidence. Just because it is harder to build analogue computers, and because it has not been done yet, does not mean that is impossible to build one that is more powerful than a digital computer.
p730, paragraph 1: The particles are indeed discrete, but their positions and velocities are continuous (at least to the limits of our measuring capability).
p730, last paragraph: I fail to see why the fact that arithmetic operations have non-local effects on digits is of any significance; as Wolfram himself points out elsewhere, size is what matters :-)
p731, paragraph 1: This seems like stacking the deck to me: compare continuous and discrete computation with a discrete measuring rod.
p733, paragraphs 1-3: Some PDEs (e.g. Navier-Stokes equations) can be thought of as generalizing cellular automata systems as the automata size tends to zero; would it then be so surprising that the PDE version can generate behavior in a finite time limit that the cellular automata system would generate as time tends to infinity?
p733, paragraph 5: "Particularly following the discoveries in this book". No. Neuronal systems are known to follow simple rules (as Wolfram describes on p.1075), and brains are made of neurons.
p1127, "History": The number in question is known as Ω;see page 1067.
p1127, "Continuum and cardinality": It is worth clarifying that "infinite lists of real numbers" must be a countably infinite list (by the fact that it makes a list).
p1130, paragraph 2: I don't know why Wolfram is claiming that getting nested patterns from continuous systems is difficult when he goes on to give one particular example and one entire (vast) class of examples.
p735, last paragraph: (Example of general theme.)
p737, paragraph 1: I'm not convinced that this assumption of un-sophisticated evolution has actually been made.
p737, paragraphs 4-5: This is my point. If you can't do prediction, then the model is not going to be that interesting.
p739, paragraph 6: Chaos theory did indeed make this observation—but it also made others.
p741, paragraphs 3, 5: Just because some convoluted initial condition for a system can generate universal computation does not in itself mean that general initial conditions produce interesting or hard-to-predict behavior. I'll concede Wolfram's point that many systems are capable of supporting universality, but almost all (in both the English and mathematical senses of the phrase) of the initial conditions do not.
p741, paragraphs 7-8: I disagree. An alternative viewpoint from more traditional science is that there has not been much success in studying complex systems because they are nonlinear, which means that breaking down the behavior into simple chunks that can be added together is not possible. Nonlinear models can still be computationally reducible (in Wolfram's sense) but still display complex behavior and difficulties in analysis.
p742, paragraph 1: This observation has also been made by the proponents of chaos theory, where the study of nonlinear systems has been compared to the study of non-elephant zoology.
p742, paragraph 3: Nonsense. Many computer models in the last twenty years have had no correlation with mathematical formulae. Artificial life, artificial intelligence, neural networks, ...
p742, paragraph 5: This example is nonsense. Just because a system can emulate another system that emulates the first system, that says nothing about the speed or efficiency of either process. [31-Oct-02] However, I should clarify that it is just this particular attempt at explanation that I object to, not Wolfram's general point that irreducibility implies impossibility of summarization.
p743, paragraph 1: The idea that universal computation shows up even with arbitrary, simple, initial conditions appears to have crept in here without any evidence or justification.
p744, paragraph 3: To clarify: in situations involving continuous mathematical formulae, the lower order digits will matter less and less in the output—and so can effectively never matter.
p745, paragraph 2: Still continuing the viewpoint that solutions to constraints have to be calculated.
p748: It is worth pointing out that just having a mathematical theory is not always in itself that helpful. Many of the equations of modern fundamental physics (general relativity, QED, QCD, etc) are extremely difficult to solve or even approximate except in simple situations. (Wolfram mentions this on p1133).
p1133, paragraph 5, left column: It is hardly the "influence of Mathematica" that has led to more systems that cannot be easily summarized in equations; more the general influence of much more computing power more easily available.
p1135, "Intrinsic limits in science": Utterly breathtaking arrogance! Limits in physics are due to a "lack of correct analysis"!
p753, paragraph 4: I'd argue that Wolfram has actually made very few discoveries about computational irreducibility—and the key discovery of universality in rule 110 was not even produced by Wolfram!
p755, paragraph 6: Chaitin makes similar points about the ubiquity of undecidability.
p760, last paragraph: Wolfram is finding solutions and then looking at what problems they correspond to, and then claiming that this approach is better than the standard one. Normally, given a function, you want to find the smallest number of operations needed to perform that operation, regardless of the size of the algorithm. Wolfram is enumerating all possible algorithms in size order, and then determining what function they perform—which allows him to make guarantees that there are no smaller algorithms that perform the same function, but does not allow him to guarantee that no algorithm performces the same function faster (despite his vague claims on p764). So...
p758, paragraph 6: Wolfram is not in fact solving problems that others have tried and failed at. He is solving problems that others have ignored as not interesting.
p1138, "Undecidability in Mathematica": I flat disbelieve Wolfram's claim that he deliberately chose not to write a Mathematica function because of undecidability concerns.
p1142, paragraph 2, left column: I have seen no evidence presented in this book for this claim that optimal algorithms are likely to have a different form than currently.
p1148, paragraph 1, left column: Presumably "at some level discrete must be used" should read "at some level discrete values must be used".
p775, paragraph 4: Mathematics has not "almost defined itself" interms of axiomatic systems; there are many areas of maths (such as much of applied mathematics) that do not take this approach. Mathematics is much more than just algebra.
p776-779: The form of mathematics that he is simulating here is that of Whitehead & Russell, which dates from the early part of the 20th century.
p781, paragraph 2: The axiom systems that Wolfram refers to typically more than just "appear" to be consistent. If there is a model that satisfies the axioms, then they cannot be inconsistent—and these theories do have models.
p785, paragraphs 5-6: This seems like a very long-winded way of proving Gödel's theorem.
p786: I'd hardly describe this as a "simple proof", given how many underlying results it relies on.
p791, paragraph 3: Again, Chaitin has made similar points.
p792, paragraph 4: Not true; many of the systems that Wolfram considers have been studied in traditional mathematics, as he indicates in the notes.
p792, paragraph 4: Mathematics ranges far wider than the traditions of geometric and arithmetic systems—for example, model theory or the vast topic of differential equations.
p793, paragraph 1: Wolfram induces confusion by switching back and forth between talking about axioms and theorems. Normally, theorems are deduced from axioms; then, if you know that a system satisfies the axioms, you are guaranteed that it will also satisfy the theorems. The aim is then to find axioms that are as general as possible (in terms of the systems that satisfy them) while still having useful consequences, in a simple form (so that verifying that a system satisfies them is easy).
p793, paragraph 4: There's a good reason why Wolfram's "new approach" is not the normal one: it is clearly more useful to try to model something specific rather than to invent an arbitrary model and then see what it might be modelling.
p1150, paragraph 4: Mathematica is hardly a serious solo contender for an alternative to standard maths. I wouldn't disagree that computation and automated proofs are becoming more important (regardless of which computer system they are produced in), but for smaller scale symbolic manipulation Mathematica's capabilities don't really exceed that of an average mathematician. Personally, I also find Mathematica notation to be singularly unhelpful, as indicated by the impenetrability of many of the examples given in the notes.
p1150, "Axiom systems": I disagree that Wolfram's results "strongly suggest" that logic is not essential; it make not make much difference to the decidability characterics of the axiom system, but it will make a huge difference to the usability.
p1150, right column, last line: As far as I can tell, Mathematica does not actually support quantifiers (except in the trivial way that it allows \[ForAll] and \[Exists] as notation).
p1153, "Other algebraic systems": I'm not sure that all of the topologists and geometers would agree that the "vast majority" of algebraic systems are groups, rings and fields.
p1154, right column, paragraph 1: Wolfram himself gives an example of a non-axiomatized mathematical system.
p1156, right column, penultimate paragraph: Wolfram persists in his delusion that Mathematica is the only computer mathematics system available.
p1157, right column, last paragraph: Interesting work towards "a general system for imitating heuristics used in human thinking" is done by Douglas Hofstadter's Fluid Analogies Research Group.
p1162, right column, top line: It's true that arbitrary cardinalities are little used, but the distinction between countable and uncountable infinities () turns up often in analysis ("almost everywhere", "set of zero measure").
p1162, right column: Aleph-one is not the cardinality of the reals (see for example chapters 6 and 8 of Enderton [1977]).
p1167, "Truth and incompleteness": It is worth being clear that most of the implications that Wolfram makes from the Principle of Computational Equivalence are actually implications from the universality and undecidability of computation.
p795, paragraph 4: I still disagree with his characterization of mathematics as consisting entirely of algebra.
p797, penultimate paragraph: To use standard terminology, we are interested in axiom systems that admit models.
p799, paragraph 3: Wolfram does not distinguish between two types of axiomatic systems. One attempts to encode all possible information about, say, the natural numbers—and so completeness is of interest. The other attempts to encode key, common, features about, say, groups—and see what can be deduced from just those general features. For this latter type of axiomatic theory, completeness is irrelevant—as Wolfram alludes to in paragraph 4 of p800.
p800, paragraph 2: It is not true that nonstandard models of arithmetic have not been constructed. See, for example Kaye [1991] or sections 5.4 and 6.3 of Manzano [1999].
p800, paragraph 5: Utter nonsense. Group theorists do not add axioms to restrict their study to a particular group (although they might add axioms to restrict to a particular class of groups, such as commutative groups).
p801, paragraph 1: I feel this is not an entirely accurate representation of the history and character of set theory.
p801, paragraph 5: In particular, the approach described allows the manipulation of systems where there are potentially an infinite number of values for the variables (for any size of infinity, too, using the Löwenheim-Skolem theorems).
p801-814: I fail to see the intent and purpose of these pages, other than the demonstration that Wolfram has access to large amounts of computer time.
p816, paragraph 4: I would suggest that ease of (human) understanding is the main reason for the particular forms of axiomatic system. For practical use, you want axioms where a) the process of exploring the space of derivable theorems is easiest and b) the process of verifying that a particular model satisfies the theory is as easy as possible. Wolfram makes a similar point to a) on p818, paragraph 1.
p820, paragraphs 5-6: Greg Egan presents a nice fictionalized account of this process in chapter 2 of "Diaspora"
p821, paragraph 6: The phenomena of computational irreducibility was already quite clear before this book.
p821, last paragraph: Not a new observation.
p1172, "Model theory": It is worth making clear that categorical theories are typically of little interest; the upward Löwenheim-Skolem theorem implies that categorical theories can only have finite models. Of more interest are k-categorical theories, where all models of cardinality k are isomorphic. Note also that all categorical theories are necessarily complete. (see chapter 7 of Manzano [1999]).
p824, last paragraph: (Example of general theme.)
p825, paragraph 5: Personally, I disagree with Wolfram's claim that an alien would have to be similar to terrestrial lifeforms for it to be considered alive.
p828, paragraph 7: (Example of general theme.)
p830, paragraph 7: Personally, I see very little similarity between the rule 110 behavior and traditional engineering systems.
p834, paragraph 6: I don't see how Wolfram can extrapolate from human development to make it "almomst inevitable" that artifacts would be constructed on an astronomical scale.
p837, paragraph 4: Although Wolfram is reasonably convincing in his claim that many systems can support universal computation, this only appears for certain very specialized initial conditions.
p837, paragraph 8: A random system could indeed generate primes—but the chances of this happening would be extremely small. If one were to observe a sequence like the primes emerging from a system, and if there were no obvious way that this could be evolved behavior that has enhanced the fitness of a self-reproducing system, then an assumption of design would be justified.
p838, paragraphs 4-5: Just because lots of systems in nature are performing computation of some form, it still does not make it likely that they will perform the exhaustive search that Wolfram mentions is required to reach the mechanism that satisfies the constraint.
p838, penultimate paragraph: It is not true that the more direct a representation is, the more likely a physical mechanism is to generate it. Imagine coming across a sequence that turned out to be the numbers of neutrons in the most stable isotope of each element in order. This is a very direct representation, but any explanation of how such a sequence could be produced accidentally is going to be byzantine. In terms of perception, this relies on the phenomenon of discreteness, which any intelligence in the galaxy is likely to be able to distinguish (for example, there is no such thing as 0.7 of a star).
p839, paragraph 7: A "few percent" of what? Signals? Actual ETs?
p840, paragraph 2: Surely the implications for technology are limited by the phenomenon of computational irreducibility implied by Wolfram's Principle of Computational Equivalence?
p840, paragraphs 5-6: (Example of general theme.)
p841, paragraph 6: Not shown in this book; already known.
p843, paragraph 2: As far as I can tell, the sum total of the "abstract knowledge" that Wolfram has built up is that there are simple cellular automata with universal behavior (and hence it is likely that universality is more common than previously suspected), and that simple cellular automata can generate both random and structured complex behavior (which is analogous to the discoveries of chaos theory).
p843, paragraph 4: My feeling of "just how often" elementary cellular automata can be applied is not very often at all, actually.
p843, paragraph 6: An even vaster amount of current technology is not emulating any natural systems—televisions, videos, bridges, computers, helicopters, ...
p844, paragraph 5: This paragraph actually makes it clear that Wolfram's theoretical equivalence of all systems that perform computation is much less relevant practically. For it is immediately obvious that there is a difference in the computational sophistication displayed by humans and rule 110.
p845, paragraph 3: (Example of general theme.)
p846, paragraph 4: The Principle of Computational Equivalence does not "now show" this; it was already well known.
p1178, paragraph 1: Wolfram claims that "it seems that" there is typically no sensitive dependence on initial conditions involved in weather forecasting. I'd like to see a reference for this; if true, it would imply that more recent approaches to weather forecasting using ensemble prediction would not actually provide distinct results across the ensemble.
p1179, "Self-reproduction": The name Fredkin is coming up again....
p1182, paragraph 1: I disagree that people assume that mathematical notation is universal, rather than just a convention. You only have to look at how logic notation has changed to see this.
p1182, paragraph 2: Again, I don't think that anyone assumes that base 2 notation is particularly fundamental. It is the smallest sensible base, and it corresponds to the current architectures for computers, and so is used as a matter of convenience.
p1182, "Computer communication": The development in communication methods typically reflects the fact that available bandwidth for transmission used to be limited, but has grown substantially (it has been observed that this growth is actually faster that that of Moore's Law for semiconductors—see for example section 3.3 of Tanenbaum [1996]).
p1183, paragraph 1: The same phenomenon applies in a number of other interpreted languages.
p1184, "Artifacts in data": It is fairly well established that chaos is not a numerical artefact—see for example the analytical solution of the logistic map, studies that obtain the same results from different numerical schemes, and the proof of chaotic dynamics in the Lorenz equations
p1185, right column, first paragraph: This discuss of purpose again reflects Wolfram's odd approach to constraints.
p1185, "Possible purposes": I disagree. If you encountered a system generating the digits of π, I think imputing a purpose would be the most sensible approach.
p1193, paragraph 1: I'm not sure what "popular options" for randomness on consumer electronics Wolfram is referring to; I can only think of the random track selection on CD players as an example.
p1196, "Philosophical implications": Again, the implication is from undecidability of the halting problem, not from the Principle of Computational Equivalence. I still feel that predictability of models is going to remain an essential component for the forseeable future.